The baseline shift operation simply subtracts a constant value from all amplitudes in the input. Baseline shifts are frequently necessary to correct small calibration errors in data recordings. It may not always be apparent when examining the input that a baseline shift is necessary. For example, the picture below is of a pressure record from an explosive test. Other than signal noise, the amplitudes of the recording appear to have a mean value of roughly 0 before the arrival of the shock front at the pressure gauge.
 

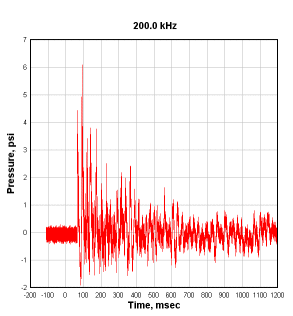
However, if the pressure record is integrated to get impulse vs. time, the pressure offset before the arrival of the shock front becomes much more obvious:

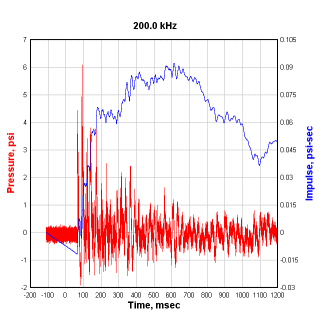
While that error in the integrated record may be small at the arrival time, when propogated across the entire record it can be very significant, as we will see in this example.

The impulse value at the arrival time of the shock front should be 0. It is not simply because of a small (in this case negative) offset in the pressure record, most likely due to a small calibration error for the pressure gauge. To correct this problem all that is needed is to subtract that small offset from the input pressure record. But what is the value of that offset? It is the sign-reversed amplitude of the impulse at the time step before the arrival time divided by the total time from the start of the recording until the arrival time.

The first step is to determine the arrival time of the shock front. DPlot's baseline shift module finds the arrival time by scanning through the input for the first amplitude that departs from the initial amplitude by more than 5% of the range in amplitudes for the total record. Why 5%? There is nothing magic about that value; it is simply chosen as a reasonable estimate for records that are not exceptionally noisy. Using these procedures, the arrival time for our example pressure record is found:

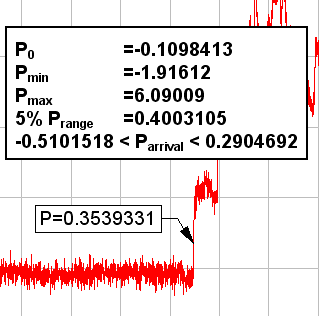
In this example, either of the previous 2 time steps could more accurately be called the arrival time of the shock, so the procedure is not perfect. But an important point to remember is that the goal is to get the integrated value at the arrival time equal to 0, not the input record. For this particular example the calculated arrival time is off by 2 time steps, or for this 200 kHz record, by 0.01 milliseconds. The contribution of the pressure record to the generated impulse record in 0.01 milliseconds is negligible, and therefore so is the small error in the calculated arrival time.

The baseline shift module then numerically integrates the input data up to the time step preceeding the calculated arrival time. Again, the goal is to get this value equal to 0. The error in the integrated record is some constant shift in the input multiplied by the time at which the error is measured minus the initial time. So the correction that should be applied to the input record is:

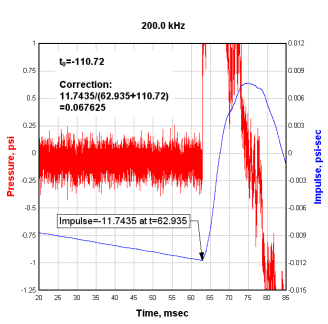
After adding that correction to the input record and re-integrating, the resulting plot shows a zero impulse at the arrival time:

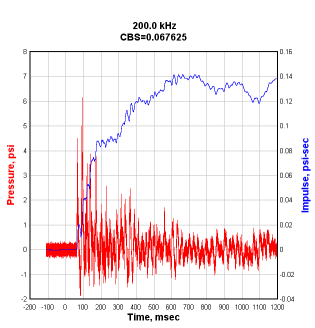
Note the difference in peak impulse from the initial plot: the corrected record has a maximum impulse of 0.1415 psi-sec, the initial record's peak impulse was 0.0924 psi-msec, or a difference of 53%.

Two qualifiers concerning this procedure should be noted:

1. If the initial amplitude in the input is significantly different than 0 (or more correctly, the baseline measurement), then the calculation of the arrival time will be off.
2. Likewise, if the input record is exceptionally noisy then there simply is no good way to programmatically determine the arrival time. For very noisy records you should perform the above steps manually.

In all cases you should never take for granted that the results of this operation will be perfect. If the resulting graph shows an integrated record significantly different than 0 at the actual arrival time, then the procedure obviously had a problem determining the arrival time and the results should not be used.