Etats liés du puits de potentiel
Commentaires :
On considère une particule de masse M dans un puits de potentiel rectangulaire.
A l'intérieur du puits ( -a < x <+a) le potentiel est nul et à l'extérieur,
il vaut V. E désigne l'énergie de la particule.
L'équation de Schrödinger
s'écrit :
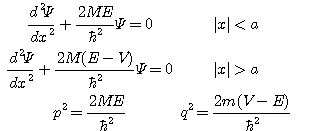
A cause des symétries du
problème, les solutions sont paires ou impaires.
Entre -a et +a, la
solution est de la forme Y = Asin(px) ou Y
= Bcos(px).
Pour x > a et pour x < -a, les solutions sont des exponentielles
décroissantes. La continuité de la fonction d'onde et de sa dérivée pour x =
±a impose que pour les fonctions paires l'équation tan(pa) = -p/q soit satisfaite
et que tan(pa) = q/p le soit pour les fonctions impaires.
Ces conditions font
que l'énergie ne peut prendre que des valeurs discrètes.
Il existe plusieurs
méthodes graphiques de résolutions de ces équations mais dans l'applet, nous
utilisons une méthode numérique de recherche de zéros.
Les constantes A et B sont calculées en
écrivant que l'intégrale de la probabilité de présence entre - l'infini et +
l'infini doit être égale à 1.
L'applet :
Les zones
de texte permettent de modifier la valeur de la largeur du puits et celle du
potentiel V. Les unités sont arbitraires (2Mh2 = 1).
Les traits bleus correspondent aux valeurs
possibles de l'énergie.
Les courbes en rouge représentent les fonctions d'onde
paires. Celles en jaune les fonctions impaires. Des cases à cocher permettent
de choisir entre la visualisation des fonctions d'onde ou celle des probabilités
de présence (carré de la fonction d'onde).
Noter que les nouveaux niveaux
apparaissent au sommet du puits et que plus l'énergie est grande plus la probabilité
de trouver la particule hors du puits augmente.
 Retour au menu.
Retour au menu.