Couplage par condensateur
Principe :
On considère le circuit suivant :

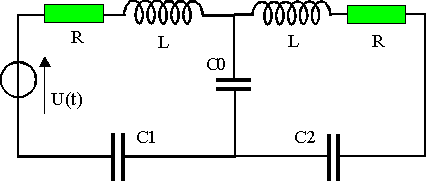
Deux circuits RLC série sont couplés par le condensateur C0.
Les deux inductances sont identiques (même L = 0,2 H et même R).
On peut faire varier la valeur du rapport C1/C2 entre 0,1 et 10 , la valeur du rapport C0/C1 entre 1 et 25 ( C1 = 1 µF) et la valeur de R (Rmini = 2 ohms).
Avec ce mode de couplage, les deux circuits ne sont pas bien individualisés et les fréquences propres des deux circuits dépendent du couplage.
Les équations du circuit sont :


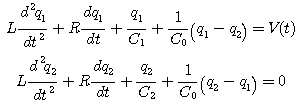
Pour le régime libre (V(t) = 0), ces équations sont intégrées avec une méthode de Runge-Kutta à l'ordre 4 pendant une durée totale de 0,1 s.
Pour l'étude du régime forcé, on se limite à l'étude du régime permanent. On calcule les valeurs des impédances complexes en fonction de la fréquence de la tension appliquée à l'entrée du circuit et on trace la valeur des courants dans les deux mailles. Selon l'usage, l'axe des abscisses est gradué en Log(w/w0). Le choix de la valeur de la pulsation w0 est un peu arbitraire mais pour conserver une certaine symétrie dans les courbes de variation des courants, on constate que le choix de la valeur w0 = (LC)-½ avec C = C0.C1/(C0 + C1) est le plus approprié.
On pourra utilement comparer ce montage avec le circuit antirésonant classique.

Suggestions :
Régime libre
Avec un rapport C2/C1 égal à 1, testez l'influence du couplage et de l'amortissement.
On observe des échanges successifs de la charge initiale entre les deux circuits avec une périodicité fonction de la valeur du couplage.
Examiner le rôle du couplage avec des circuits peu différents ou très différents.
Régime forcé
Le programme fait le calcul de l'amplitude maximum des courants (normes des courants complexes).
Étudier le rôle du couplage sur les fréquences de résonance quand les deux circuits sont identiques.
Étudier le rôle du couplage sur les fréquences de résonance quand les deux circuits sont peu différents ou très différents.
Voir le rôle de l'amortissement sur l'aspect de l'acuité des résonances des circuits.

Il faut valider après la dernière entrée dans les zones de texte pour que les valeurs saisies soient prises en compte.

Retour au menu électricité.