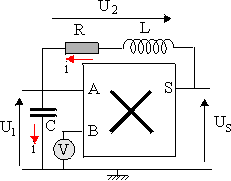
Circuit RLC paramétrique

Ld²q/dt² + R.dq/dt + (1 - KV)q/C = 0

on pose l = R/2L, w₀² = 1/LC.
L'équation devient l'équation de Mathieu : d²q/dt² + 2l.dq/dt + (1 + K.v.coswt)q = 0 .
L'effet produit par la tension de commande V est équivalent à une variation de la capacité de C. Tout ce passe comme si l'épaisseur du condensateur variait selon une loi de la forme e = E(1 - KV).
L'étude analytique (assez délicate) de cette équation montre qu'il existe des résonances autour des fréquences 2f₀, f₀, 2f₀/3 ...
En dessous d'une valeur seuil de v, le système oscille avec une amplitude faible. Au delà du seuil, l'amplitude de l'oscillation diverge avec une croissance exponentielle qui est limitée en pratique par le multiplieur. L'amortissement du circuit agit sur la valeur du seuil.
Au voisinage de certaines valeurs des paramètres,  le fonctionnement de ce circuit est très sensible aux valeurs des conditions initiales.

Le programme calcule l'évolution du potentiel aux bornes du condensateur par intégration numérique de l'équation différentielle mais la valeur maximum de la charge du condensateur est limitée pour tenir compte des performances réelles du multiplieur.
Commandes :
Des zones de texte permettent la saisie des valeurs des paramètres du circuit du montage. Le bouton permet de visualiser soit l'évolution de la tension U₁ en fonction du temps soit la courbe donnant l'intensité en fonction de la charge (équivalent d'un diagramme de phase).
Les valeurs de L et C sont choisies pour que la fréquence propre soit égale à 1 kHz. A cette fréquence, le fonctionnement du multiplieur ne pose aucun problème  de déphasage.  Attention, il faut valider la dernière valeur saisie.
 Etude :
 Pour w/w₀ voisin de 2 examiner l'évolution de la valeur du seuil. Examiner le rôle de l'amortissement.
Les régimes de fonctionnement d'un tel circuit sont multiples : examiner par exemple les cas suivants et faire varier légèrement les paramètres autour des valeurs proposées.