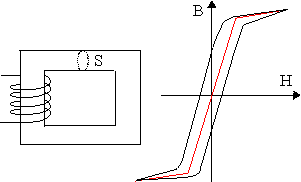
On considère un transformateur bobiné sur un matériau magnétique doux. Le noyau a une section S et une longueur moyenne L. Le primaire comporte N spires et sa résistance est R.
On alimente le circuit primaire avec une tension sinusoïdale et on veut déterminer le courant qui circule dans le primaire quand le secondaire est ouvert.

Les équations du circuit sont :
u(t) = U.sin(wt + q)
F(t) = S.B(t) avec B(t) = f(H(t))
H(t).L = N.I(t)
u(t) = N.dF(t)/dt + R.I(t)

C'est un système non-linéaire à cause de la relation qui relie le champ H et l'induction magnétique B.
Pour un matériau magnétique, le cycle d'hystérésis permet de représenter l'évolution de ces deux grandeurs.Son allure dépend du matériau et de son histoire antérieure.

En négligeant l'hystérésis, on peut modéliser le cycle d'un matériau doux par trois segments de droites (courbe en rouge). Il est alors possible de calculer numériquement l'évolution du courant en fonction de la tension. Si la saturation du noyau est atteinte, il se produit une surintensité qui peut être très grande et qui s'amortit lentement. Cette surintensité dépend de la phase de la tension au moment de la fermeture du circuit. Les effets sont maximum pour une phase nulle ou égale à 180°. Pour une phase égale à 90°, on obtient immédiatement le régime permanent.
Les courbes de l'intensité sont déformées à cause des hypothèses simplificatrices retenues. On peut améliorer les choses en simulant la courbes B = f(H) par 5 segments de droites.

La prise en compte de l'hystérésis permet de justifier le fait que pour un transformateur non chargé, la forme du courant primaire s'écarte beaucoup d'une sinusoïde.