Prisme
Le prisme :
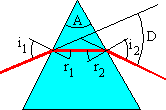
L'indice du milieu qui constitue le prisme a un indice n > 1. Le prisme d'angle au sommet A est
dans un milieu d'indice 1. Un rayon incident émerge après deux réfraction en
faisant l'angle D avec sa direction initiale. Etablissez les relations :
sin i1 = n sin r1
sin i2 = n sin r2
r1 + r2 = A
D = i1 + i2 - A
Pour qu'il existe un rayon émergent, il faut que r2 soit inférieur à
l'angle limite l tel que sinl
= 1/n sinon, il y a réflexion totale sur la seconde face du prisme.
En écrivant les différentielles des quatre équations du prisme, montrez que
la déviation présente un minimum Dm quand i2 = i1.
En déduire l'expression de n en fonction de A et de Dm.
La variation d'indice avec la longueur d'onde l
peut être représentée par la formule de Cauchy n = a + b/l².
En différentiant les relations du prisme, montrez que le rouge est moins dévié
que le violet par le prisme.
L'applet :
La liste permet de choisir entre la visualisation de la déviation (source monochromatique) , de
la dispersion du prisme (lumière blanche) ou de la courbe D = f (i1).
Une zone de saisie permet de modifier la valeur de l'indice n. L'angle A est égal à 60°.
Pour changer l'angle d'incidence sur le prisme,
glissez avec la souris le gros point, situé à l'origine du rayon incident, le long du bord vertical.
Dans le mode "dispersion", les valeurs de l'indice en fonction de la longueur d'onde utilisée sont :
n = 1,612 (0,768 µm) ; 1,623 (0,589 µm) ; 1,629 (0,540 µm) ; 1,635 (0,486 µm) ; 1,646 (0,434 µm)
Courbe D = f (i1) : Elle
met bien en évidence le fait que la déviation présente
un minimum. Pour les angles d'incidence inférieurs à l'angle limite
(repéré par le trait bleu vertical) il y a réflexion totale
sur la face de sortie du prisme. Montrer que pour cet angle, la déviation
à la même valeur que pour une incidence égale à 90°.
La souris permet de déplacer un curseur horizontal qui indique
la valeur de la déviation correspondante.
 Retour au menu.
Retour au menu.
