Correction de l'astigmatisme des lentilles
Principe :
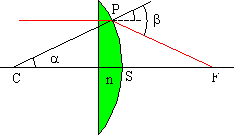
On considère une lentille plan-convexe de rayon R = 10 cm, éclairée en lumière parallèle par un faisceau
de rayon 5 cm. L'indice n de la lentille est égal à 1,5.
Pour tracer les rayons, il suffit de remarquer que l'angle d'émergence est :
b = Arcsin(n.sin(a))puis de construire la droite de pente a = tan(b - a) passant par le point de
réfraction.
On constate que les rayons éloignés de l'axe sont trop réfractés pour avoir stigmatisme.
Lentille à gradient d'indice.
On considère une lentille dont l'indice varie avec la distance à l'axe optique. L'indice sur l'axe
est égal à 1,6 et l'indice de chaque strate de la lentille est calculé pour que chaque émergent PF'
qui coupe l'axe en F', passe par le même point F (avec SF = 16,6 cm). La courbe de variation de l'indice (graduations de 1,3 à 1,6)
est tracée en fonction de la distance à l'axe (graduations de 0 à 5 cm).
En pratique, à chaque pas, on cherche la valeur de n qui annule SF - SF'.
Lentille à courbure variable.
On considère cette fois une lentille dont le rayon de courbure varie afin que les émergents passent
par le même point F (avec SF = 9 cm). Le profil de la lentille obtenue est tracé (cyan) avec celui de la
lentille sphérique correspondante (blanc).
Commentaires :
Les solutions obtenues ne sont pas réellement satisfaisantes car on ne corrige pas l'achromatisme
de la lentille et la solution n'est valable que pour les rayons parallèles à l'axe.
Les solutions avec plusieurs lentilles d'indices différents donnent de meilleurs résultats.
Toutefois, on utilise souvent des lentilles asphériques moulées comme condenseur ou comme lentille frontale
des objectifs à courte focale et grande ouverture.
 Retour au menu "optique géométrique".
Retour au menu "optique géométrique".
