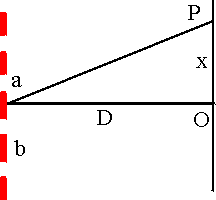
On veut déterminer l'intensité de la lumière en un point P du plan d'observation distant de x de l'axe du système.
On pose : u = p.x.b/(l.D) et k = b/a.
On peut montrer (voir un cours d'optique) que l'intensité lumineuse en P est le produit de la fonction diffraction d'une fente par la fonction d'interférence
:
IP = [sin(u/k).sin(Nu)/(sin(u).u/k)]2.
Le programme calcule l'intensité dans le plan d'observation pour x compris entre +5
mm et -5 mm et trace la courbe correspondante.
L'applet
:
Deux listes de choix permettent de choisir le nombre
de fentes et la valeur de la longueur d'onde utilisée.
Les cases à cocher permettent de visualiser soit la figure d'interférence
des n sources, soit la figure de diffraction d'une seule source,
soit le phénomène global.
Deux ascenseurs (faire glisser le curseur avec la souris) permettent de faire varier la
largeur des fentes (a) et leur écartement (b).
Vérifier que
seul l'écartement des fentes agit sur la valeur de l'interfrange et que la largeur
des fentes modifie la figure de diffraction.
Vérifier que l'accroissement
du nombre de fentes induit une concentration de la lumière autour des valeurs
entières de u.
Remarque : Pour le tracé,
les intensités sont normalisées ( Imax = 1). En réalité, le phénomène est d'autant
plus lumineux que la largeur des fentes est grande.