Calculating Energy v.s. Distance Curves for F₂ and "He₂"

The bond scanning function provided in the Iconc options makes this straightforward and the results are plotted using EXCEL.

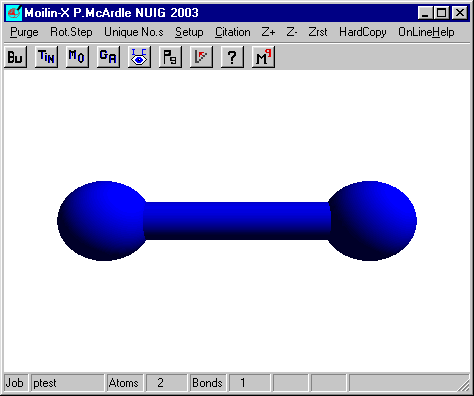
Build F₂ and measure the F-F bond length using the button and stop this function using . If you do not know how to do this look at the tutorial on Building and Optimizing BF₃.
Return to display mode and you should have.

Click to bring up the Iconc menu.

Select NewInput and on dialog 15

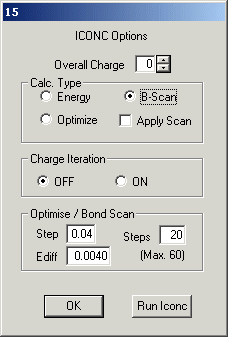
select B-Scan and set Steps to 60 and click Run Iconc. When the bond scan is complete exit Moilin and in Oscail select Edit / Edit.GEO the top of the file will look like the following.

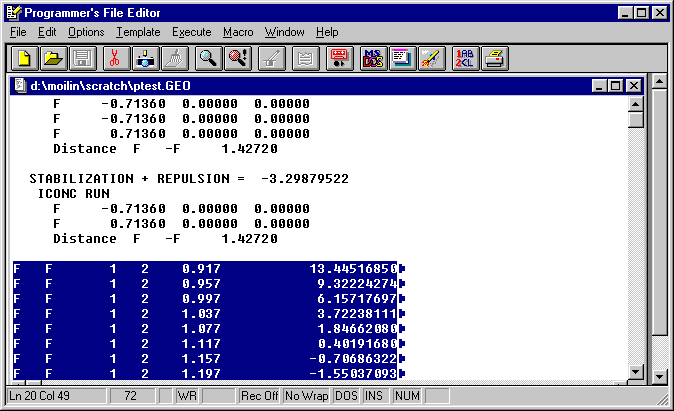
Select the portion of the file which has the scan results (60 lines) as shown and use Edit on the PFE menu to Copy to the clipboard. Close PFE and start EXCEL. In EXCEL select Edit and Paste. Without clicking any other buttons click Data then Text to Columns and Finish. This should give.

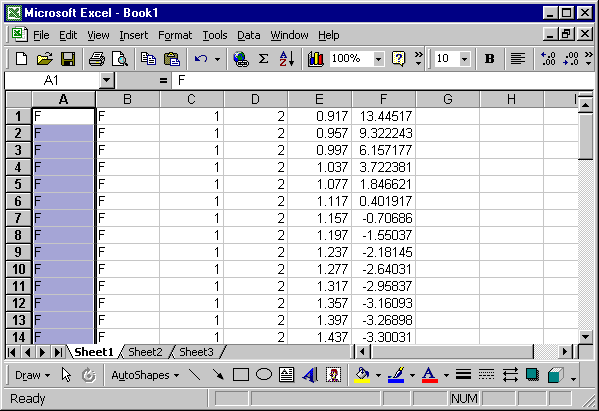
Select the last two columns (E and F) and click the chart wizard button . Selecting X-Y (Scatter) and the second option on the left followed by Finish should give.

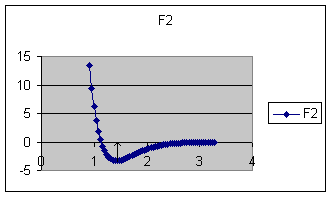
This curve shows that the minimum energy is at the normal F-F bond distance (1.43 Å). Curves of this type can be produced by the Morse Function ( E(r) = De(1 - e^(-a(r-re))^2  P.M. Morse 1929) hence the term Morse Curve.
Repeat this process for hypothetical "He₂" and the following curve should result.

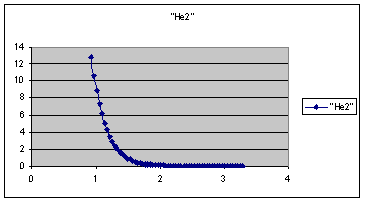
There is clearly no bond here.

Back