

 |
The Used Generators |  |
The generators of a space-group type include the identity , the centering vectors for non-primitive lattices and a special selection of symmetry elements (the so-called generators selected), which combination determines all other symmetry elements. The derived symmetry elements define the commonly used general positions, if any will be multiplied with the atomic coordinate (x,y,z). The most important advantage of the new generation (in contrast to the former DOS version) is the small size of necessary information for each space-group type. This decreases spelling mistakes too, but if such exist a detection is very easy because one half or two third of all generated positions must be wrong.
To describe all space-group types and the different settings it's enough to define 15 generator types. These correlate with the following symmetry elements: -1, 2x, 2y, 2z, 2[110], 2[1-10], mx, my, mz, mxxz, mx-xz, 3, 3[111], 4, -4. The generator itself consist of generator type and an additional translation part defined by the translation vector of the symmetry element and their shift from the origin. The generators can be used to create all special positions, too (see: generation of atomic positions). Using the Wyckoff notation a multiple generation will be prevented. There only some generators will be used in dependence of the local symmetry, respectively. The order of these or which must be selected is declared in the symmetry file pcwspgr.dat. There only a simple encoding has been developed. In maximum 5 generators gi must be given (exclusively the lattice centering vectors and the identity). The equation for the calculation of the code number is:
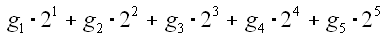 |
If one doesn't need a generator (except the identity and lattice centering vectors) the encoded number is 20=1. In case of selection of the first and the third generator the encoding results
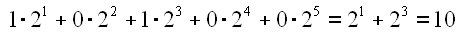 |
Federal Institute for Materials Research and Testing
Unter den Eichen 87, D-12205 Berlin,
Germany