EP7_15C.RTF
Seventh European Powder Diffraction Conference (EPDIC-7), Barcelona, Spain, 20-23 May 2000
Oral contribution OC57: 13:00, 23 May 2000 (revised 16 June 2000 by the author for posting on the CCP14 website)
Progress in Automatic Powder Indexing
Robin Shirley, School of Human Sciences, University of Surrey, UK
Introduction
In this talk we’ll be looking at:
What powder indexing is and why it’s necessary;
Parameter space vs index space;
Why indexing is difficult, including the character of its solution space;
A survey of methods and programs, including more recent approaches;
The Crysfire suite: indexing for non-specialists;
Some current issues and opportunities;
And finally, a live Crysfire demonstration.
Before proceeding to these points, let me begin by saying that success in powder indexing, perhaps more than in any other aspect of powder diffraction, depends critically on the resolution and accuracy of one’s observed data. [This note was added in response to a comment by the session chairman, Jan Visser, but it is in any case one to which I most strongly subscribe.]
What is Powder Indexing?
It’s the process of inductive reasoning from internal regularities within the set of observed d* values, by which their indices can be inferred and the three-dimensional reciprocal lattice reconstructed, yielding the previously unknown unit cell parameters.
Why is Indexing Necessary?
Indexing is increasingly required for both scientific and industrial work:
Modern methods for structure solution and Rietveld refinement allow ab initio structures to be solved from powder data for most solid phases of moderate size and complexity, but only if the unit cell is known. Indexing is increasingly the limiting step in this process.
Polymorphs of the same compound often differ in pharmaceutically important properties like solubility and bioavailability. Guiding a new drug through regulatory processes and preparing patents needs a thorough characterisation of its polymorphs. Indexing thus takes on commercial significance, since it’s much easier to defend patents on a particular polymorph if one can show unambiguously that it’s a single solid phase.
One can only be sure such patterns represent single solid phases if they’ve been fully indexed.
Parameter Space vs Index Space
The process of generating a powder pattern from a set of cell constants has 6 degrees of freedom: the 3 sides and 3 angles of the general unit cell, or their 6 equivalents in reciprocal space, or, more usefully, the 6 powder constants QA to QF that give the linear relation as shown.
From these equations, indices can be assigned if the cell is known, or the cell calculated if the indices are known. Inferring the indices is equivalent to determining the cell parameters, so that indexing can be done either in a 6-dimensional parameter space or an equivalent 3N-dimensional integer-valued index space.
Why is Powder Indexing Difficult?
Since structure analysis involves many unknown parameters, while a unit cell only contains 6, why isn’t this a trivial problem?
Well, 6 parameters are already enough to place exhaustive, brute-force methods out of reach, at least in the general triclinic case, since they’d take years of computer time. And there are deeper reasons.
Indexing an unknown powder pattern looks like the logical inverse of generating the pattern, but it isn’t. Powder indexing isn’t reversible, and it’s inductive rather than deductive. Pattern generation has at most 6 degrees of freedom – fewer in high symmetry, but this doesn’t hold for indexing.
Thus to generate a cubic pattern needs only one constant – the cell side a. If this were reversible, an unknown cubic cell could be found from a single powder line, which is plainly absurd, since its indices wouldn’t be known. Even in high symmetry there are still 6 metrical degrees of freedom – to call a pattern orthorhombic is just shorthand for saying 3 of its constants are now known.
The cell sides might need doubling or more, requiring a further 3 order-fixing degrees of freedom. And there may be an instrumental degree of freedom due to uncertainties in specimen displacement, and hence in the effective zero of 2
Thus strictly the indexing process has at least 9 and often 10 degrees of freedom, while, as we’ll see, there may be only some 20-30 useful observed lines, so it’s not as over-determined as we’d like.
As d* increases, the number of reciprocal lattice points increases as its cube. This quickly overwhelms even synchrotron resolution, giving overlaps that increase rapidly with 2
q . Modern pattern-decomposition methods help, but resolved peaks remain more reliable than those extracted from multiple overlaps.Calculated Qhkl values depend on the second power of their indices, becoming increasingly sensitive with 2
q to small cell changes. This helps cell refinement, but not indexing, since the match of each obs line to the nearest calc line becomes unstable. So as 2q rises, assigned indices are increasingly likely to be wrong, even if the cell is roughly correct, which for least-squares purposes is worse than not using those lines at all.Lines beyond the first 20 or 30 contribute little indexing information, because they place few constraints on possible cells. That’s why one can’t power through the degrees of freedom problem simply by measuring more lines.
4) Solution space problems
Lastly, it turns out that the relevant solution space is often hostile and resists global optimisation, especially in low symmetry.
The Character of Indexing’s Solution Space -
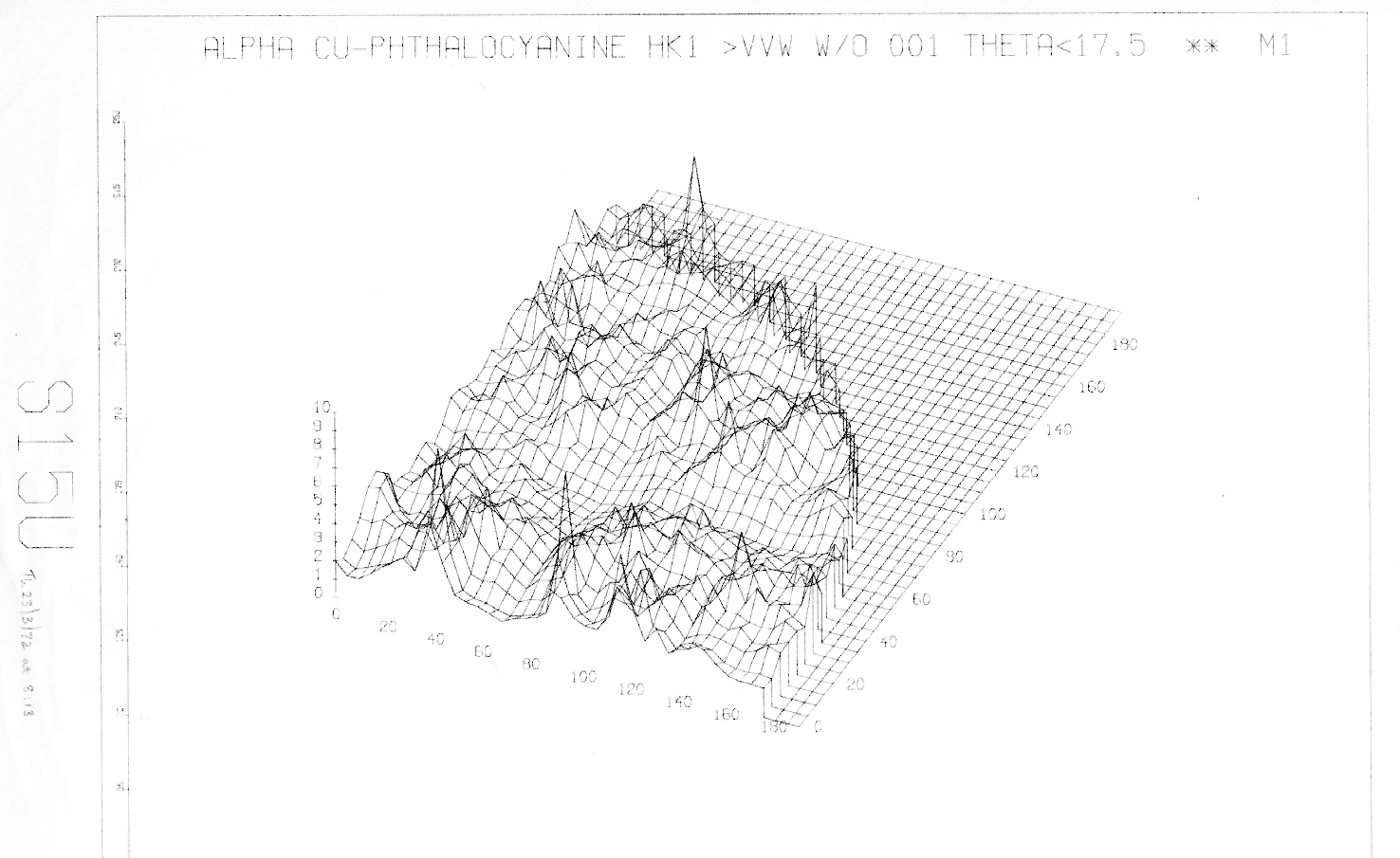
By plotting figure-of-merit against lattice parameters for an observed pattern, we can explore its solution hyperspace, as shown in the diagram.

Fig 1. M1 surface in the QD/QE (i.e.
The map shows the localised, spiky and irregular nature of maxima in indexing’s solution space. This is unhelpful for most global optimisation methods, which for good performance need to:

Fig 2. WM3 contour plot near the origin of the QD/QE section for
a -Cu phthalocyanineAnother issue – pseudo-symmetry - is raised in this contour plot, from an enlarged region of the sharpened merit surface, near the origin of the section we’ve just seen.
a
-Cu phthalocyanine is triclinic but strongly pseudo-monoclinic, so that the large peak shown in red is very close to, but not on, the QD axis (i.e. b * is almost 90º), while g * (not shown here) is exactly 90º within experimental error. This sort of thing can be confusing for programs that impose assumptions about metrical symmetry (and for humans too).
A Survey of Methods and Programs
Rather than review these individually, I’ve prepared comparative tables, starting by classifying the methods, including two global optimisations – simulated annealing and the diffusion equation - that to my knowledge haven’t yet been tried. The diffusion equation should suit these spiky solution spaces.
Method Space Exhaustive Status Program(s) available
Zone indexing Parameter No Mature Yes (2)
Successive dichotomy Parameter Yes Mature Yes (1+)
Grid search Parameter Yes Semi-mature Yes (1)
Combined heuristic Parameter Semi Mature Yes (2)
Genetic algorithms Parameter No Developing Yes (1)
Simulated annealing Parameter No Not yet tried No
Diffusion equation Parameter No Not yet tried No
Scan/covariance Par. (both) To monocl. Developing Yes (1)
Index heuristics Index No Mature Yes (2)
Index permutation Index Yes Mature Yes (1)
(The list is not claimed to be complete. Only symmetry-general methods are included)
The list is arranged first by search space, then from established methods to newer ones. Eight out of ten work primarily in parameter-space.
Then there’s their search strategy. Exhaustive methods can be used to rule out crystal systems and screen for high-symmetry solutions, but get increasingly time-consuming in low symmetry. About half the methods contain some exhaustive element and 2 are capable of being fully exhaustive.
The last columns give an idea how mature the programs are for each method, and how many are available.
The next table identifies the programs. They’re underlined if within Crysfire, and in round brackets if not generally available. You can see there’s a much wider choice than the classic trio of ITO, DICVOL and TREOR: 13 are listed, of which 11 are currently available and 8 supported by Crysfire.
Space Method Programs using this method
Parameter Zone indexing ITO12, FJZN6
Successive dichotomy DICVOL91, [in part: LZON, LOSH]
Grid search SCANIX, (Powder49)
Combined heuristic LZON, LOSH
Genetic algorithms AUTOX, (W.P.G.A.: Belmonte et al)
Simulated annealing (not yet implemented)
Diffusion equation (not yet implemented)
Par. (both*) Scan/covariance EFLECH/INDEX
Index Index heuristics TREOR90, TMO [=KOHL]
Index permutation POWDER [=TAUP]
(Underlined if supported by Crysfire, in round brackets if not generally available)
* EFLECH/INDEX operates in parameter space down to monoclinic, then switches to index space for triclinic.
Moving to specific programs, this summary table includes authors and operating system environments – mostly DOS, which is still good for small, numerically intensive programs, though I expect there are more 32-bit Windows and Linux versions out there than I’ve shown.
Program Author(s) Method Space Exhaustive O/S
ITO12
Visser Zone index. Par No DOS +?FJZN6 Visser & Shirley Zone index. Par No DOS
DICVOL91 Louër & Boultif Dichotomy Par Mainly* DOS +?
SCANIX Paszkowicz Grid search Par Yes DOS/ANSI
(Powder49) Shirley Grid search Par Semi Mainframe
LZON Shirley/Louër/Visser Comb. heur. Par Semi DOS
LOSH Shirley & Louër Comb. heur. Par Semi DOS
AUTOX Zlokazov Genetic alg. Par No DOS/extender
(W.P.G.A.) Harris** Genetic alg. Par No Unix
EFLECH/INDEX Bergmann Scan/covar. P/(I)* Mainly* DOS,Win,Linux
TREOR90 Werner Index heur. Ind No DOS +?
TMO [=KOHL] Kohlbeck Index heur. Ind No DOS +?
POWDER [=TAUP] Taupin Index perm. Ind Yes DOS +?
* EFLECH/INDEX operates in parameter space down to monoclinic, then switches to index space for triclinic. Like DICVOL91, it is exhaustive only down to monoclinic.
** Ken Harris told me at the meeting that he is now the primary contact for the genetic algorithm indexing program reported by Kariuki et al (1999), J. Synchr. Rad., 6, 87-92. As its name had not yet been finalised, I have listed it here as W.P.G.A. (for Whole-Profile Genetic Algorithm program).
Next their typical run times in the three commonest crystal systems, and how far they operate automatically - only completely so for 7, all of which are within Crysfire. For 5 of these, run times are broadly independent of symmetry, but of course not for the two using primarily exhaustive strategies.
Program Orthor. Monocl. Tricl. Comments
ITO12
2 sec 2 sec 2 sec AutomaticFJZN6 3 sec 3 sec 3 sec Automatic
DICVOL91 <5 sec 2-30 min mins-hours* Automatic, very volume-dependent
SCANIX c.30 min (?10 min) n.a. User guided in monoclinic
(Powder49) c.15 min in each case (PC Equivalent times) User guided
LZON 5-15 min in each case Automatic
LOSH <1 min <1 min <1 min User guided
AUTOX ?1 min ?10 min ?1 hour Semi-automatic in practice?
(W.P.G.A.) Run times said to be lengthy (Alpha / SGI workstation)
EFLECH/INDEX 15 min 1 hour 15 min c.Automatic, exhaustive to monoclinic
TREOR90 <1 min <1 min <1 min Automatic
TMO [=KOHL] <1 min <1 min <1 min Automatic
POWDER [=TAUP] <20 sec 1 hour+ Very long Automatic
(Typical run times are offered here as a rough guide, but may vary considerably with data & settings)
* Additional notes:
Daniel Louër has queried the correctness of the triclinic run time of "hours+" for DICVOL91 in my original table. He said that students in his laboratory (using very high quality triclinic data) usually only require a few minutes. In his opinion any triclinic search taking over 15 minutes is having problems and should be aborted.
This raises an important issue concerning how DICVOL91 has been optimised, particularly in low symmetry. It is excellent for general use down to orthorhombic and for relatively low-volume monoclinic cells. However, at higher volumes in monoclinic, and especially in triclinic, it seems to me that DICVOL91 has been optimised more for guidance by experienced users than for automatic use by non-specialists. The run-time entries in the table above are intended as a guide for general users, not for experienced users who may well be able to take short cuts, and they also assume good-quality laboratory datasets that are more typical than the very high quality ones measured in Daniel’s laboratory.
In response to Daniel’s comments, I have carried out a test run with DICVOL91 using a difficult triclinic Guinier-camera dataset showing some line broadening, approaching this as far as possible like a non-specialist user carrying out an ab initio search. Using 0.06° 2Theta limits (realistic in this case), DICVOL91 completed a search down to triclinic for volumes up to 2000A3 in 7.5 hours, but did not find a convincing solution, although a 347A3 cell with M20=24.8 existed within its search space and was found by LZON in 2.5 minutes. The best DICVOL91 solution was a monoclinic cell with volume 684A3 (1.97V), so that it might have been a monoclinic approximation to a 2V derivative cell. Reducing the 2Theta limits to the default of 0.03° shortened the run time to 14 minutes, without finding either the 347A3 triclinic cell or the previous 684A3 monoclinic cell.
This brings out several points: (1) that DICVOL run times are very sensitive to the 2Theta limits, so that it performs much better with very accurate data (and without impurity lines, which are not permitted); (2) that its searches are only exhaustive down to monoclinic, so that it may well miss solutions lying within its search path in triclinic; (3) that for triclinic datasets it is worth trying other programs such as ITO, TREOR, KOHL, FJZN6 and LZON before attempting a triclinic run with DICVOL.
Daniel also warns of the danger of launching DICVOL runs with relatively large 2Theta limits (such as 0.06°), since DICVOL is then more likely to halt after finding a false solution in a lower volume shell, and so not continuing and finding the correct cell in a subsequent shell (this didn’t happen in my test, but easily could have). In such cases, an experienced user knows to restart the run from the next volume shell in order to check for the existence of further possible solutions, but such considerations may not occur to a non-specialist.
Finally an attempt to capture their particular strengths and weaknesses – a kind of consumer guide. Note how the different programs complement each other.
Tolerates
Tolerates: Random
Program Impurities Errors Comments
ITO12
Yes No Optimised for low-symmetryFJZN6 Yes No As for ITO12, but more robust
DICVOL91 No Slows For screening to orthor./monocl., no impurities
SCANIX Yes Slows? Under development, user guided
(Powder49) Slows Maybe (Superseded by LZON)
LZON Slows Slows Best for dominant-zone cases
LOSH Slows Slows User-guided, faster than LZON
AUTOX ?Slows ?Slows Many optional user settings
(W.P.G.A.) Yes Slows Uses whole profile, under development
EFLECH/INDEX Yes Slows Uses full peak-fit covariance matrix
TREOR90 Yes No Specialises in very accurate impure data
TMO [=KOHL] Yes Yes Fast, useful for high & low symmetry
POWDER [=TAUP] Slows ?Slows For screening down to orthorhombic
(Though nominally automatic, in practice AUTOX often needs some user guidance)
Some unfamiliar ones come out well here. For example, I’d single out FJZN6 as a more robust alternative to standard ITO, and LZON as strongest at handling pathological, multi-solution cases. And also KOHL’s rare combination of speed and tolerance of both impurities and random errors, though not pathological cases. All three deserve wider use.
Indexing for Non-Specialists: the Crysfire Suite (Shirley)
Crysfire simplifies indexing for non-specialists by offering a unified semi-automatic environment from which indexing programs can be called and their results evaluated.
Modified versions of eight indexing programs (ITO12, FJZN6, DICVOL91, TREOR90, POWDER [TAUP], TMO [KOHL], LZON and LOSH) are incorporated, under the overall control of CRYS, a data-handling front-end and indexing wizard.
The results from each indexing program are displayed, and one-line summaries of its solutions are added to an overall summary file and presented in descending order of plausibility, as we shall see in a minute.
Crysfire is distributed free for non-commercial use from the CCP14 website (www.ccp14.ac.uk).
Some Current Issues and Opportunities
1) Incorporation of instrument parameters
Uncertainties over the effective specimen position are common, even for synchrotron data. At low angles this mainly shows as a zero error, so can be corrected by self-calibration (Shirley, 1980; PowderX: Dong, 1999), either as a fixed 2q zero term, or more exactly as one varying with cos q , though the difference is small at low angles. It could also provide a heuristic for distinguishing correct zones, since these should have the same correction term.
2) Incomplete-solution criteria
Figures of merit like M20 and FN rely on the solution being complete and accounting for all observed lines. Often this is enforced by excluding "unindexed" lines – observed lines that fail to agree closely enough with calculation (thus modifying the data to fit the model, not a prudent practice).
The Ishida & Watanabe PM figure of merit doesn’t assume a complete model, allowing solutions to be developed and tested incrementally, and one phase indexed in the presence of others.
3) Sparse datasets (High-P/High-T)
There’s a growing need to index datasets with fewer observed lines than usual, due to unavoidable experimental restrictions, but this needs to be reconciled with the degrees-of-freedom arguments raised earlier.
4) Scale independence – can one index a protein pattern?
Formally the indexing problem is scale independent – it uses only relative dimensions and doesn’t care if everything gets 10 times bigger. This has been verified experimentally. But it’s well known that in practice large cells make indexing harder. Although indexing is scale independent, instrument resolution and accuracy are not, so if the d-spacings are 10 times bigger, the data must be 10 times better. And yes, Bob von Dreele has indexed some protein patterns, at least in high symmetry - Crysfire now includes scale-shifting to support this.
5) Co-operation between programs
Indexing-related software tends no longer to operate in isolation, but to co-operate with other programs. Thus the Laugier & Bochu CHEKCELL program can browse the list of trial solutions in a Crysfire summary file and assign probable spacegroups.
Crysfire demonstration
Now for a live demonstration of indexing the easy way, using Crysfire – it should take under 2 minutes (time me).
[This showed an ab initio indexing run launched from within Crysfire using KOHL on a Y2(oxalate)3.2H2O test dataset. A 648.7A3 C-centred monoclinic cell with M20=113 was found in 8 seconds, with the whole demonstration completed within 1 min 45 sec.]
Conclusions
The powder-indexing problem is now well understood, though not always solved. Powerful programs are available and becoming more widely used. However, in view of its growing importance, much remains to be done - to make these tools more accessible and better integrated, to address difficult problems of mixed phases and sparse data, and to explore some of the new approaches that I’ve mentioned.