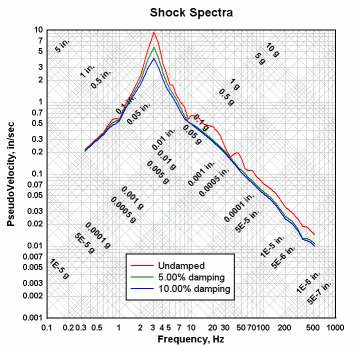
A tripartite plot (also known as "four coordinate paper") consists of a logarithmic scale on both the X and
Y axes and two additional logarithmic scales that are derived from the X and Y axes by some fixed relationship. It is typically used in vibration
analyses to determine the peak responses (acceleration, velocity, and displacement) of many different frequency damped,
single degree of freedom systems
exposed to support motions. Those support motions might be due to earthquakes, explosions, vehicle collisions, etc. Generally a tripartite plot used
in this manner will consist of frequency in Hertz on the X axis, psuedo velocity (maximum relative displacement times frequency in radians) on the Y
axis, displacement lines at 45 degrees to the X axis, and acceleration lines at 135 degrees to the X axis.
There are three important regions on this plot. On the left is the maximum deflection or required rattle space. The center shows the frequency or frequency range where the maximum velocities are generated. That region is sometimes flattened, depending on the frequencies associated with the support motion. On the right the spectrum slopes downward along the maximum acceleration line. These three regions show the needed rattle space, the frequency range for which the shock is severe, and the peak acceleration. For explosive events that peak acceleration line is often critical when evaluating shock-sensitive equipment.
For shock spectra plots, acceleration and displacement values are given by d = v/(2pf) and
a = -2pfv,
where
a=acceleration
d=displacement
f=frequency
v=velocity
In the more general case,
45° lines = A * Y / X
135° lines = B * X * Y
where A and B are constants.
By default DPlot displays X as frequency in Hertz, Y as velocity in inches, acceleration in g's, and displacement in inches. Presets for the constants A & B are included in DPlot to alternatively display velocity in feet/second, millimeters/second, centimeters/second, or meters/second and displacement in feet, millimeters, centimeters, or meters. For other units you can specify the constants A & B. The following table is presented to provide examples of proper values for those constants:
| X | Y | 45° | 135° | A | B |
| Hertz | inches/sec | inches | in/sec^2 | 0.1591549 | 6.2831853 |
| Hertz | inches/sec | inches | g's | 0.1591549 | 1.6273972E-02 |
| Hertz | feet/sec | feet | g's | 0.1591549 | 1.9528766E-01 |
| Hertz | mm/sec | millimeters | g's | 0.1591549 | 6.4070659E-04 |
| Hertz | cm/sec | centimeters | g's | 0.1591549 | 6.4070659E-03 |
| Hertz | meters/sec | meters | g's | 0.1591549 | 6.4070659E-01 |
If X represents the period of the oscillation rather than the frequency in cycles/second, the above relationships are simply reversed: The 45° lines represent acceleration and the 135° lines represent displacement:
| X | Y | 45° | 135° | A | B |
| seconds | inches/sec | g's | inches | 1.6273972E-02 | 0.1591549 |
| seconds | feet/sec | g's | feet | 1.9528766E-01 | 0.1591549 |
| seconds | mm/sec | g's | millimeters | 6.4070659E-04 | 0.1591549 |
| seconds | cm/sec | g's | centimeters | 6.4070659E-03 | 0.1591549 |
| seconds | meters/sec | g's | meters | 6.4070659E-01 | 0.1591549 |
Privacy Policy