
This page is meant to be an introduction to the field of Quasicrystals in order to educate the interested reader on some basic concepts in this relatively new branch of Crystallography. The more advanced reader may proceed to other sites and sources on quasicrystals.
|
|
In classical crystallography a crystal is defined as a threedimensional periodic arrangement of atoms with translational periodicity along its three principal axes. Thus it is possible to obtain an infinitely extended crystal structure by aligning building blocks called unit-cells until the space is filled up. Normal crystal structures can be described by one of the 230 space groups, which describe the rotational and translational symmetry elements present in the structure. Diffraction patterns of these normal crystals therefore show crystallographic point symmetries (belonging to one of the 11 Laue-groups). In 1984, however, Shechtman, Blech, Gratias & Cahn published a paper which marked the discovery of quasicrystals. They showed electron diffraction patterns of an Al-Mn alloy with sharp reflections and 10-fold symmetry. The whole set of diffraction patterns revealed an icosahedral symmetry of the reciprocal space. Since then many stable and meta-stable quasicrystals were found. These are often binary or ternary intermetallic alloys with aluminium as one of the constituents. The icosahedral quasicrystals form one group and the polygonal quasicrystals another (8,10,12-fold symmetry). We can state that quasicrystals are materials with perfect long-range order, but with no three-dimensional translational periodicity. The former is manifested in the occurrence of sharp diffraction spots and the latter in the presence of a non-crystallographic rotational symmetry.
Since quasicrystals lost periodicity in at least one dimension it is not possible to describe them in 3D-space as easily as normal crystal structures. Thus it becomes more difficult to find mathematical formalisms for the interpretation and analysis of diffraction data. For normal crystals we can assign three integer values (Miller indices) to label the observable reflections. This is due to the three-dimensional translational periodicity of the structure. In order to assign integer indices to the diffraction intensities of quasicrystals, however, at least 5 linearly independent vectors are necessary. So we need 5 indices for polygonal quasicrystals and 6 indices for icosahedral quasicrystals. We can call them generalized Miller indices. The necessary n vectors span a nD-reciprocal space. Therefore there is also a nD-direct space in which a structure can be built that gives rise to a diffraction pattern as it is observed for quasicrystals. To put it simply we can say that in the higher-dimensional space we can describe a quasiperiodic structure as a periodic one. The actual quasiperiodic structure in the 3D-physical space can then be obtained by appropriate projection/section techniques. Thus it is enough to define a single unit cell of the nD-structure. The contents of that nD-unit cell consists of "hyperatoms" (occupation domains, ..) in analogy to the atoms in a normal unit cell. This enables us to describe the whole quasicrystal structure with a finite set of parameters. If we described it in 3D-space only, we needed thousands of atoms to obtain a representative volume segment of the whole structure as well as all parameters that go with it (eg. thousands of positions).
Example for a 1D-quasiperiodic sequence (Fibonacci chain)
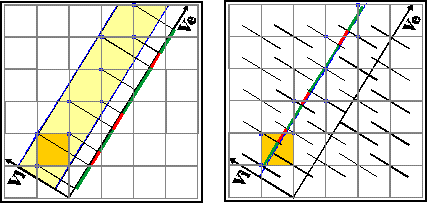 In order to elucidate this
concept with a simple example lets have a look at a 1D-"quasicrystal"
in form of a Fibonacci chain, which is a quasiperiodic sequence
of short (red) and long (green) segments. We embed this 1D-"quasicrystal"
in a 2D-"higher dimensional space" which in this case
has the form of a simple square lattice. One unit cell of the
higher-dimensional space is filled yellow. The axes show the
orientation of the two orthonormal subspaces Ve, Vi. The slope of
Ve with respect to the 2D-lattice has to be an irrational one. In
this case it is tau=1.618... The left image demonstrates the
projection method, where we have a strip of projection with
finite width. All points of the 2D-lattice inside this strip are
projected onto the external space Ve, thus giving the
quasiperiodic sequence (red,green..). The right image shows the
section method in which a hyperplane (here a 1D-line) that is
parallel to Ve cuts the higher-dimensional space. The occupation
domains that are attached to each of the lattice points (here:
bars) intersect with the hyperplane (here: line) thus producing
the same quasiperiodic sequence as in the left picture. These
occupation domains (here: bars) extend parallel to the internal
space Vi. We can generalize this to nD cases with n=5,6,.. In
that case the internal space would be (n-3)-dimensional and the
occupation domains would be two-dimensional (eg.polygons) or
three-dimensional (eg. polyhedra).
In order to elucidate this
concept with a simple example lets have a look at a 1D-"quasicrystal"
in form of a Fibonacci chain, which is a quasiperiodic sequence
of short (red) and long (green) segments. We embed this 1D-"quasicrystal"
in a 2D-"higher dimensional space" which in this case
has the form of a simple square lattice. One unit cell of the
higher-dimensional space is filled yellow. The axes show the
orientation of the two orthonormal subspaces Ve, Vi. The slope of
Ve with respect to the 2D-lattice has to be an irrational one. In
this case it is tau=1.618... The left image demonstrates the
projection method, where we have a strip of projection with
finite width. All points of the 2D-lattice inside this strip are
projected onto the external space Ve, thus giving the
quasiperiodic sequence (red,green..). The right image shows the
section method in which a hyperplane (here a 1D-line) that is
parallel to Ve cuts the higher-dimensional space. The occupation
domains that are attached to each of the lattice points (here:
bars) intersect with the hyperplane (here: line) thus producing
the same quasiperiodic sequence as in the left picture. These
occupation domains (here: bars) extend parallel to the internal
space Vi. We can generalize this to nD cases with n=5,6,.. In
that case the internal space would be (n-3)-dimensional and the
occupation domains would be two-dimensional (eg.polygons) or
three-dimensional (eg. polyhedra).
 Before quasicrystals were discovered in
1984 the british mathmatician Roger Penrose devised a way to
cover a plane in a nonperiodic fashion using two different types
of tiles. An example can be seen on the left. The tiles (rhombii)
are arranged in a way that they obey certain matching rules. An
equivalent tiling can be obtained for a 3D-arrangement. This is
called a 3D-Penrose Tiling, which is made up of rhombohedrons
instead of the rhombii. Such 2D and 3D-tilings have several
important properties, such as the selfsimilarity, which means
that any part of the tiling occurs again within a predictable
area (or volume). After the discovery of quasicrystals in 1984 a
close resemblance was noted between the icosahedral quasicrystal
and the 3D-Penrose pattern. By putting atoms at the vertices of a
3D-Penrose pattern one can obtain a Fourier Transform which
explains very well the diffraction patterns of the found Al-Mn
quasicrystal. In a similar way one can use 2D-Penrose Tilings (left)
to approximate a decagonal quasicrystal, which in a simple case
consists of two layers with local 5-fold symmetry, which are
rotated by 18 degrees so that the projection along the rotation
axis gives a 10-fold symmetry. As stated above it is also
possible to derive the vertices of such tilings using the nD-space
approach (n>3). In this case we can obtain such a tiling by a
projection of a nD periodic lattice (eg. hypercubic lattice).
Before quasicrystals were discovered in
1984 the british mathmatician Roger Penrose devised a way to
cover a plane in a nonperiodic fashion using two different types
of tiles. An example can be seen on the left. The tiles (rhombii)
are arranged in a way that they obey certain matching rules. An
equivalent tiling can be obtained for a 3D-arrangement. This is
called a 3D-Penrose Tiling, which is made up of rhombohedrons
instead of the rhombii. Such 2D and 3D-tilings have several
important properties, such as the selfsimilarity, which means
that any part of the tiling occurs again within a predictable
area (or volume). After the discovery of quasicrystals in 1984 a
close resemblance was noted between the icosahedral quasicrystal
and the 3D-Penrose pattern. By putting atoms at the vertices of a
3D-Penrose pattern one can obtain a Fourier Transform which
explains very well the diffraction patterns of the found Al-Mn
quasicrystal. In a similar way one can use 2D-Penrose Tilings (left)
to approximate a decagonal quasicrystal, which in a simple case
consists of two layers with local 5-fold symmetry, which are
rotated by 18 degrees so that the projection along the rotation
axis gives a 10-fold symmetry. As stated above it is also
possible to derive the vertices of such tilings using the nD-space
approach (n>3). In this case we can obtain such a tiling by a
projection of a nD periodic lattice (eg. hypercubic lattice).
In short, we can regard quasiperiodic tilings as frameworks that give quasicrystal structures when filled up with atoms in an appropriate way.
quasiperiodic in two dimensions (polygonal or dihedral quasicrystals)
There is one periodic direction perpendicular to the quasiperodic layers.
quasiperiodic in three dimensions, no periodic direction
new type (reported in Nature, Nov.2000)
The symmetry that determines the type of the quasicrystal is first seen in its diffraction pattern. Below some simulations of diffraction patterns are shown, which could represent either electron diffraction patterns or the zeroth layers of precession photographs (X-ray):
 octagonal QC |
 decagonal QC |
 dodecagonal QC |
Below there is a simulation for a Laue pattern (X-ray) from an icosahedral quasicrystal, whereby the x-ray beam is along one of the five-fold axes.
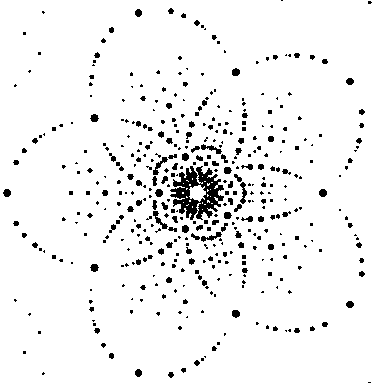
icosahedral QC
see also my Fourier transform gallery
below there is a link to a Java applet that calculates Fourier transforms from quasiperiodic tilings in analogy to diffraction patterns from two-dimensional quasicrystals
| octagonal
QC: V-Ni-Si |
decagonal QC:
Al-TM (TM=Ir,Pd,Pt,Os,Ru,Rh,Mn,Fe,Co,Ni,Cr)
|
| dodecagonal
QC: Cr-Ni |
icosahedral QC:
Al-Mn |
| new type: Cd-Yb * stable binary quasicrystal |
* stable phases exist
| selected
area electron diffraction (SAED) |
obtain reciprocal space information (symmetry, point group) |
| convergent beam electron diffraction (CBED) | determination of the point group & space group |
| high
resolution transmission electron microscopy
(HRTEM) |
real structure information
(below decagonal Al-Mn-Pd)  |
| X-ray diffraction techniques | Film methods: Laue, Precession,
Debye-Sherrer Quantitative measurement: Powder diffractometer, Four-circle diffractometer |
| neutron diffraction | obtain partial structure factors to assist structure refinement |